Landova integrální metoda

Úvod

Při simulaci dlouhodobých přírodních dějů v rozsáhlých 3D oblastech v dlouhých časových úsecích je nutné pro hodnocení věrohodnosti předpovědí kromě přímých výpočtů provádět řadu alternativních simulací, analýz citlivosti a dalších typů analýz. To má za následek potřebu velkého množství výpočetního výkonu a výpočetního času. Tento problém se zvlášť zřetelně projevuje v oblasti simulací scénářů budoucího šíření kontaminace v okolí hlubinného úložiště radioaktivního odpadu, kde simulované oblasti dosahují plošně několik kilometrů čtverečních v mocnosti několika set metrů a simulované časové úseky jsou desítky až stovky tisíc let.

Přestože výpočetní kapacita hardwaru stále roste a stále výkonnější superpočítače umožňují provádět více a náročnějších simulací, zůstává snižování výpočetní náročnosti nutnou součástí modelování. To bývá často prováděno dvěma cestami - zjednodušováním koncepce modelů, tj. zanedbáváním některých fyzikálních a chemických jevů při simulacích, nebo redukcí 3D transportní úlohy na 1D úlohu transportu jednou nebo více preferenčními cestami.

Zde představovaná integrální metoda reprezentuje postup snižování výpočetní náročnosti redukcí dimenze transportní úlohy. Provádí ji však jinak než volbou preferenční cesty. Je založena na analýze výstupů z původního 3D transportního modelu a identifikaci sdružených parametrů, které však mají fyzikální význam a rozměr, a konstrukci ekvivalentního 1D modelu simulujícího průnik kontaminantu horninovým prostředí všemi cestami v 3D modelu zároveň. Jeho výstupy jsou velmi dobře srovnatelné s výstupy 3D modelu a proto je možno na něm provádět velká množství srovnávacích a alternativních výpočtů, z nichž případně některé mohou být pro účely odstranění nejistot ověřovány výpočty na plném 3D modelu.

Použití integrální metody tak umožňuje redukci výpočetní náročnosti transportního modelu bez nutnosti zjednodušení popisu prostředí nebo omezení zahrnutých fyzikálních jevů. Pro realizaci integrální metody je nutné sestavit 3D model transportu, avšak řadu 3D simulací je v průběhu modelování možno nahradit simulacemi v ekvivalentním 1D modelu. To snižuje výpočetní náročnost práce, umožňuje provést více analýz během stejného času a nesnižuje přesnost predikcí.

Landova integrální metoda

Integrální metoda byla vyvinuta pro účely hodnocení dlouhodobé bezpečnosti hlubinného úložiště radioaktivních odpadů. Na Obr. 1 je koncepční schema kompartmentu „geosféra“, ze kterého Integrální metoda vychází.

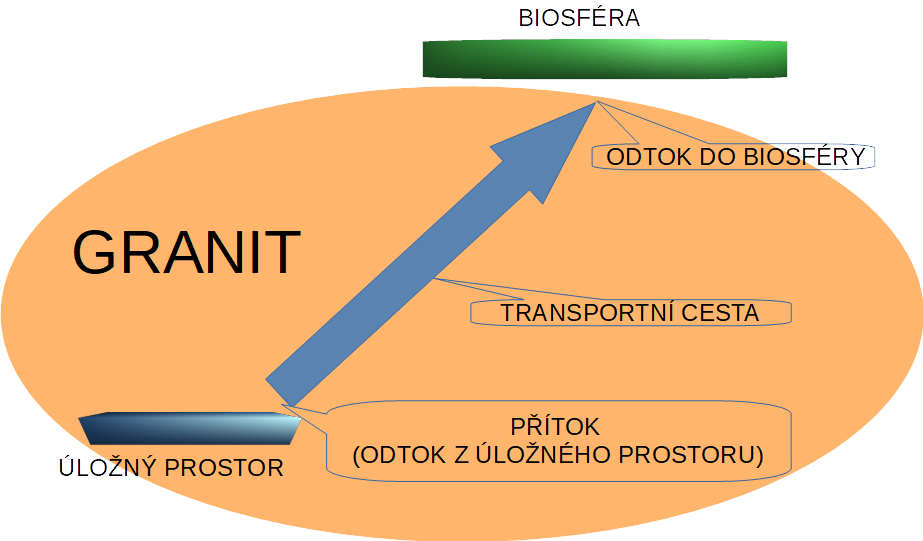
Obr. 1: koncepční schema kompartmentu „geosféra“

Metoda má dvě části, první je získání charakteristických vlastností a transportních parametrů horninového prostředí, druhá pak jejich použití v modelu se sdruženými parametry.

Tato metoda tedy umožňuje získání charakteristických vlastností a transportních parametrů horninového prostředí (kompartmentů „geosféra“) jako jsou např. doba toku, průtoky nosného média (podzemní vody), délka toku, podélná disperzivita a další.

Přestože byla tato metoda vyvíjena pro hodnocení hlubinných úložišť, je použitelná na jakýkoli 3D model transportu kontaminantů, kdy je potřeba hodnotit jejich dopad na životní prostředí, např. pro přípovrchová úložiště radioaktivních odpadů, skládky nebezpečných odpadů atd.

První část – získání parametrů z výsledků 3D modelu proudění a transportního modelu

Integrální metoda má jisté požadavky na výpočet 3D modelu. Výpočet je prováděn jako odezva na jednotkový skok koncentrace stopovačů v elementech označených jako zdrojové.

Pro testování jsme použili čtyři stopovače, nesorbující, středněsorbující, vysocesorbující a nesorbující radioaktivní (s vhodně zvoleným poločasem přeměny vzhledem k transportnímu času).

Výpočty byly prozatím provedeny bez difuze. S difuzí bude počítáno v předpokládaném budoucím vývoji této metody.

Na základě analýzy původní 3D sítě a výsledků transportního modelu a modelu proudění (tzn. z odezvy na jednotkový skok) jsou stanoveny následující souhrnné parametry:

přítok (tj. odtok podzemní vody z prostou uloženého odpadu do okolní horniny)
odtok (tj. odtok kontaminované vody z hranice modelu)
ředění (tj. podíl odtok/přítok)
délka toku
objem transportní cesty
porozita transportní cesty
kontaminované plochy
odtokové kontaminované plochy

V dalším kroku je provedena numerické derivace odezev na jednotkový skok – tím jsou získány odezvy na Diracův impulz. Z odezvy na Diracův impulz jsou získány další parametry:

doba toku
koeficient hydrodynamické disperze
podélná disperzivita

Všechny tyto parametry jsou stanovovány i pro části modelů, např. pro element s největší koncentrací, element s největším odtokem kontaminantů, jednotlivá povodí atd. Lze také z větší části vyřadit numerickou difuzi, a některé numerické chyby modelu.

Na základě výše zmíněných parametrů lze provést výběr (zúžení výběru) perspektivních lokalit. Tyto parametry jsou srozumitelné a charakteristické pro každou počítanou lokalitu.

Druhá část – interpretace získaných parametrů v modelu se sdruženými gradienty

Podle výsledných hodnot získaných Integrální metodou lze nastavit komponentu „Pipe“ v SW GoldSim. je nutné pouze dopočítat hodnotu parametru „cross area“ (tedy průřez komponenty) z doby toky, délky, porozity a odtoku.

Výsledek takovéhoto nastavení je na Obr. 2, kde modré křivky jsou výsledné z 3D modelu ve Flow123d a zelené křivky z jedné komponenty „Pipe“ nastavené výšepopsaným způsobem. Na tomto obrázku je vidět, že jsou to výborné výsledky, dostačující pro bezpečnostní analýzu, když přihlédneme k velkému množství dalších nejistot.

Přesto jsme takto nastavenou komponentu „Pipe“ dále optimalizovali, pomocí optimalizační funkce zabudované přímo v GoldSimu. Optimalizovali jsme dva parametry, tedy dobu toku (potažmo průřez, „cross area“) a podélnou disperzivitu. Jako optimalizační kritérium byl nastavena suma integrálů kvadrátu rozdílu koncentrací podle Flow123d a optimalizované komponenty „Pipe“ pro všechny čtyři počítané stopovače. Výsledné křivky optimalizované komponenty „Pipe“ jsou na Obr. 2 červenou barvou a jsou téměř totožné s modrými křivkami podle Flow123d.

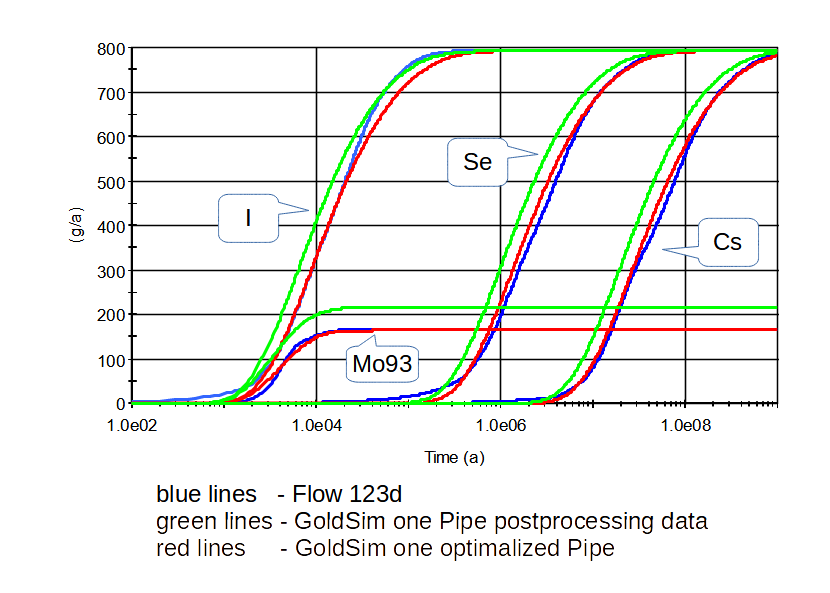
Obr. 2: ukázka výsledků integrální metody, porovnání s výstupem transportního modelu Flow123d pro čtyři různé stopovače (modré křivky), výstupu jediné komponenty „Pipe“ nastavené podle výsledných hodnot parametrů získaných pomocí integrální metody (zelené křivky) a výstupu jedné komponenty „Pipe“, která má optimalizovanou dobu toku (tzn. průřez – parametr „cross area“) a disperzivita (červené křivky)

Závěr

Integrální metoda dává velice kvalitní výsledky, které jsou potřebné pro výběr lokality hlubinného úložiště a jeho bezpečnostní analýzu. Interpretace těchto výsledků ve zjednodušeném modelu se sdruženými gradienty dává též vynikající výsledky a potvrzuje správnost tohoto postupu.

Následné použití modelu se sdruženými parametry výrazně sníží nároky na výpočetní čas umožní provést mnoho variant výpočtů a mj. provést citlivostní analýzu.